How decentralized and resilient is the Stellar network? And how can we compute network parameters and properties?
By André Gaul and Jörg Liesen.
We investigated these questions in a research project conducted at the TU Berlin and sponsored by an academic research grant of the Stellar Development Foundation. Main results of the project include:
- Thorough mathematical analysis of the FBAS consensus model underlying the Stellar network.
- Derivation and Python implementation of algorithms for quorum enumeration, quorum intersection and intactness of nodes.
- Derivation and numerical evaluation of centrality measures for the FBAS consensus model. (A key observation is that the Stellar network has evolved towards decentralization by reshaping the nodes and trust decisions in 2019 and 2020.)
Below we give an overview of the results for a broader audience. You can read the complete papers on arxiv:1912.01365 and arxiv:2012.03913. The Python package Stellar Observatory contains implementations of the algorithms from the project.
Background: Consensus Models
The main idea of blockchain technology, which originates in Satoshi Nakamoto’s Bitcoin Whitepaper from 2008, is that a network of participants (the nodes) maintain a replicated, shared, and synchronized digital database in a decentralized way, the distributed ledger. No central party has the authority on the content of the ledger. Changes to the ledger (the transactions) are recorded in blocks which point to previous blocks, thus forming a chain of blocks. The nodes replicating the ledger need to reach consensus on the next block so that it can be included in the ledger. The mechanism for reaching consensus is formalized in the underlying consensus model.
The Stellar Consensus Model
The Stellar consensus model is called Federated Byzantine Agreement System (FBAS) and was introduced by David Mazières in 2016. It is based on quorum slices and quorums, and the basic idea can be explained as follows:
A person has several different groups of people as friends, for example at work, in a sports club, neighbors, or family members. Suppose that this person agrees with some statement when an entire group of friends agrees with it. Each such group is called a quorum slice of the person. A quorum then consists of people, so that for each of them at least one group of their friends (a quorum slice) is contained in the quorum. This could be any of the different groups of friends, but for each member of the quorum it needs to be an entire group. A quorum therefore can be interpreted as a subset of the people that “trusts itself”. Quorums are the sets (of people) that can ratify statements in this network. Consensus among all participating people means that two contradictory statements can not be ratified. This is guaranteed if any two quorums have at least one common member, which is called the quorum intersection property.
In an FBAS we have abstract nodes instead of people, but the principles remain the same. In our mathematical work, we have made an effort to present a coherent formal description of these principles and illustrate them with many examples, ranging from small “academic” cases to the current Stellar network.
Mathematical Analysis
The mathematical structure of the FBAS is very rich, and even networks consisting of very few nodes can be highly complex. For example, while we write this article, the core (or “top tier”) of the Stellar network consists of (only) 23 nodes, and there are 1,900,544 quorums!
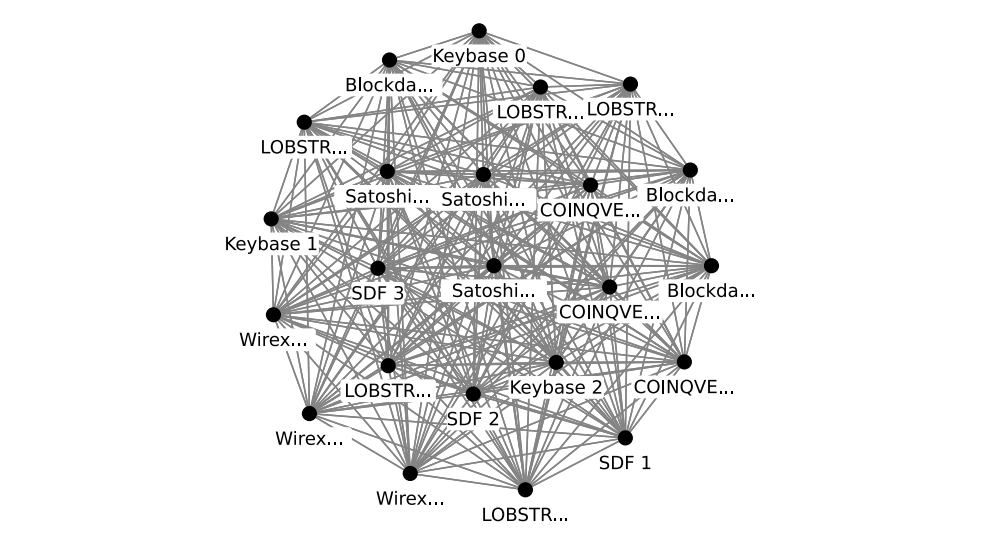
Common mathematical tools to address such challenging problems are model reduction and the analysis of special model problems. We applied both in this project.
Reduction to the Trust Graph
Every FBAS can be reduced to the mathematical structure of a directed graph, which we call the trust graph. When node B is contained in any of node A’s quorum slices, then this graph contains a link (or edge) from A to B, which indicates that A trusts B. Thus, we consider only simple links between trusting parties instead of the potentially more complicated quorum slices. While being only a reduced model, the trust graph gives valuable insights into the FBAS structure. In particular it can help to identify the important strongly connected components (SCC). We showed that checking the integrity of the entire FBAS reduces to checking only the so-called maximal SCCs. If there is only one maximal SCC, we call it the greatest SCC. In the current Stellar network, the greatest SCC coincides with the “top tier” on stellarbeat.io (see above).
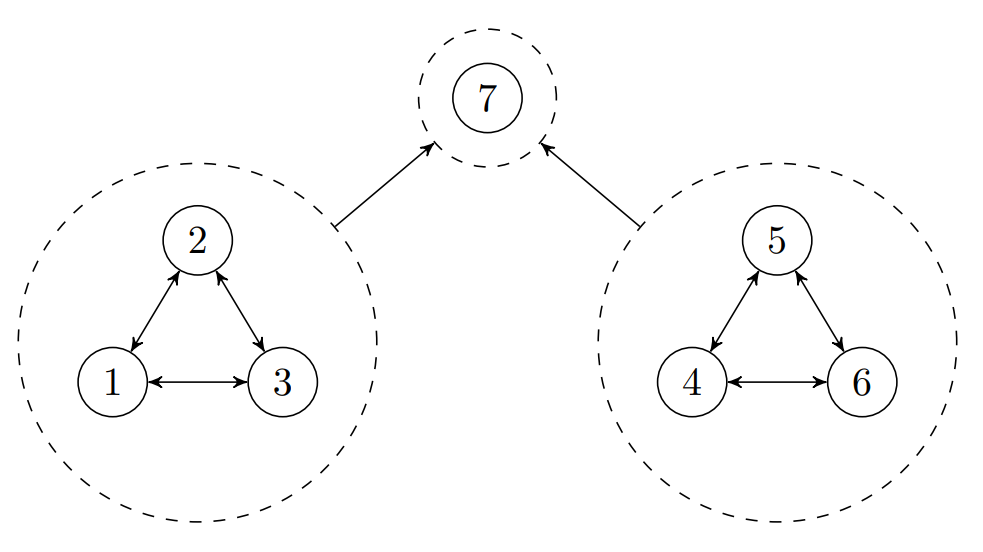
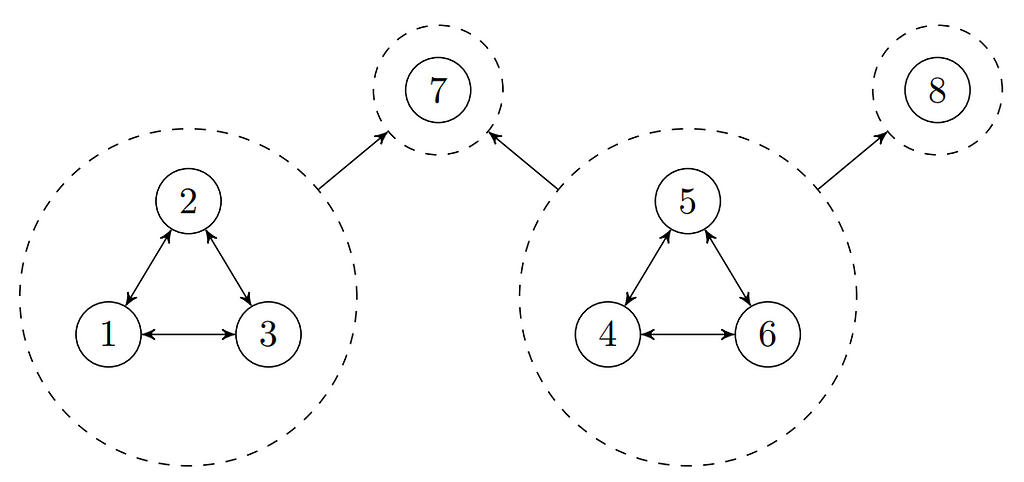
Simple and Symmetric FBAS
We introduced special FBAS model cases called simple and symmetric FBAS whose properties can be fully analyzed. This approach has the general educational aspect, that a complicated theory is easier to understand using appropriately simplified models. The insights into the general FBAS which we obtained from our special models yield transparent proofs of some mathematical results about the quorum intersection property, and a clear comparison of the FBAS with traditional Byzantine fault tolerance mechanisms.
Intactness of Nodes
An important question is how resilient an FBAS is against failed, misconfigured or malicious, in short ill-behaved nodes. If such ill-behaved nodes negatively impact other (well-behaved) nodes, then these other nodes are befouled by the ill-behaved nodes. Nodes that are not befouled are called intact. We thoroughly analyzed the intactness property and introduced a model which allows to study the probability that nodes are intact in different scenarios of ill-behaved nodes. Using several such scenarios we analyzed the resilience of different FBAS structures. We found that in terms of probabilistic intactness, our model of the simple and symmetric FBAS is superior to hierarchical FBAS structures.
Algorithms and Implementations
Checking whether an FBAS has the crucial quorum intersection property is NP-complete, and hence is computationally as difficult as solving the famous Traveling Salesman Problem. Exact solution algorithms for such problems involve brute force searches, and are feasible only for small problem sizes.
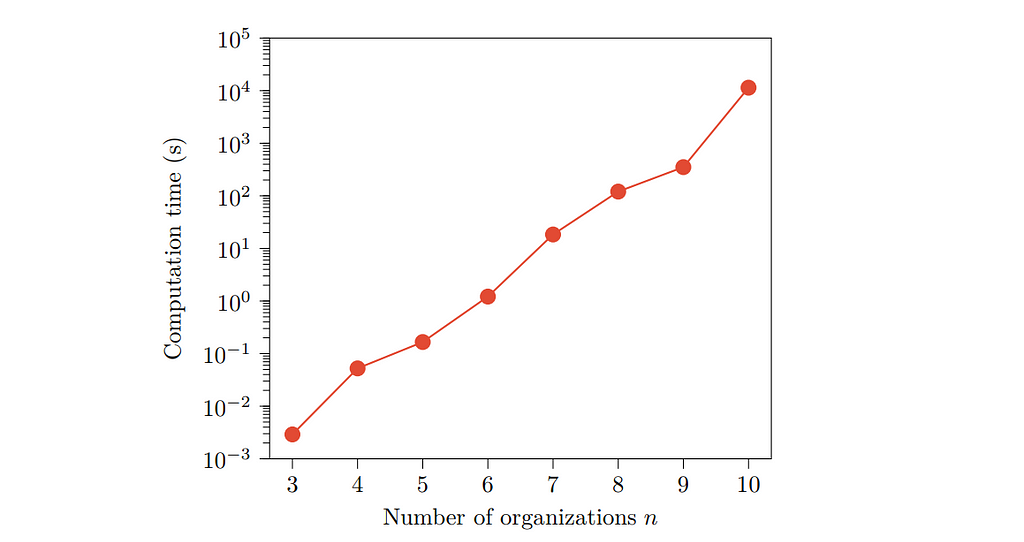
While we cannot escape the overall computational complexity, our model reduction strategies based on the trust graph and on identifying the relevant SCCs lead to simplifications in the enumeration of quorums and hence to faster computations for the quorum intersection problem. We have extended the original approach of Lachowski, who has shown that entire branches of the problem can be skipped.
Based on our algorithm for the quorum intersection problem we also derived and implemented an algorithm for computing which nodes of an FBAS remain intact when a given subset of the nodes becomes ill-behaved.
All algorithms from the project are implemented in the Python package Stellar Observatory.
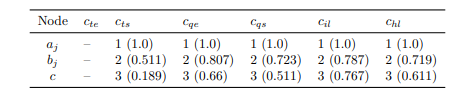
Centrality of Nodes
An essential question about the FBAS is whether the individual and hence decentralized trust decisions of the nodes lead to a network that overall can also be characterized as decentralized. The level of (de-)centralization in networks can be assessed using centrality measures, which we studied for the FBAS.
Centrality measures are well established for networks that are represented by graphs or hypergraphs. We have applied the ideas from this area (in particular eigenvector and subgraph centrality) to obtain centralities based on the trust graph as well as the quorum structure of an FBAS. These centralities have some disadvantages since both representations are significant simplifications (or model reductions) of the actual FBAS.
We also introduced an FBAS-specific centrality based on the intactness of nodes. The idea of the intactness-based centrality is that a node should be central when its ill-behavedness leads to befouldness of many other (central) nodes. This centrality suffers from the NP-completeness of the computational problem, but usually gives more refined information than the other two approaches.
Moreover, the results from our analysis show that the Stellar network evolved towards decentralization between 2019 and 2020 by reshaping the greatest SCC (“top tier”).

References
- Mathematical Analysis and Algorithms for Federated Byzantine Agreement Systems
- Centrality of Nodes in Federated Byzantine Agreement Systems
- Stellar Observatory
Research project team: Prof. Dr. Jörg Liesen (project head), Dr. André Gaul, Ismail Khoffi, Dr. Torsten Stüber (Satoshipay)
Researching the Mathematics Behind the Stellar Consensus Protocol was originally published in Stellar Community on Medium, where people are continuing the conversation by highlighting and responding to this story.

